Carmichael numbers that are products of Carmichael numbers
The following file contains the 203737 Carmichael numbers below 1024 that are
products of Carmichael numbers, together with these factors:
carmichael_products.txt
(13 MB).
After each Carmichael number its number of prime factors is shown in brackets.
There are 1396 Carmichael numbers up to 1024 that are the product of three
Carmichael numbers (and maybe also of two or four), they are in this file:
carmichael_products_three.txt.
Of those, 442 are not a product of two or four Carmichael numbers, in the file they are marked with *;
953 are, besides being a product of three, also a product of two Carmichael numbers, in the file they are unmarked;
and one is, besides being a product of three, also a product of four Carmichael numbers (but not of two),
in the file it is marked with **.
There is exactly one Carmichael number below 1024 that is the product of four Carmichael numbers:
521649490603448721200401 = 75361 × 252601 × 488881 × 56052361,
and there are no Carmichael number below 1024 that are the product of more than four Carmichael numbers.
Counts
The table below shows the counts per number of decimal digits d
and number of product representations m.
| total | m=1 | m=2 | m=3 | m=4 | m=5 | m=6 | m=7 | m=8 | m=9 | m=10 | m=11 | m=12 | m=13 |
|---|
| d= 9 | 1 | 1 | | | | | | | | | | | | |
|---|
| d=10 | 2 | 2 | | | | | | | | | | | | |
|---|
| d=11 | 7 | 6 | 1 | | | | | | | | | | | |
|---|
| d=12 | 5 | 5 | | | | | | | | | | | | |
|---|
| d=13 | 22 | 20 | 2 | | | | | | | | | | | |
|---|
| d=14 | 50 | 47 | 2 | 1 | | | | | | | | | | |
|---|
| d=15 | 103 | 99 | 3 | 1 | | | | | | | | | | |
|---|
| d=16 | 212 | 206 | 6 | | | | | | | | | | | |
|---|
| d=17 | 509 | 495 | 13 | 1 | | | | | | | | | | |
|---|
| d=18 | 1099 | 1056 | 40 | 1 | 1 | | 1 | | | | | | | |
|---|
| d=19 | 2308 | 2204 | 95 | 7 | 1 | 1 | | | | | | | | |
|---|
| d=20 | 4946 | 4722 | 204 | 7 | 9 | 4 | | | | | | | | |
|---|
| d=21 | 10676 | 10147 | 482 | 30 | 15 | 1 | | 1 | | | | | | |
|---|
| d=22 | 23323 | 22232 | 953 | 87 | 41 | 7 | 1 | 1 | 1 | | | | | |
|---|
| d=23 | 50661 | 48142 | 2239 | 158 | 88 | 16 | 6 | 9 | | 1 | | 1 | 1 | |
|---|
| d=24 | 109813 | 104487 | 4672 | 385 | 195 | 48 | 15 | 6 | | 3 | 1 | | | 1 |
|---|
| total | 203737 | 193871 | 8712 | 678 | 350 | 77 | 23 | 17 | 1 | 4 | 1 | 1 | 1 | 1 |
|---|
The table below shows the counts per number of prime factors of the Carmichael factors representations.
| 3+3: | 464 | | | | | | | | | | | | | | | | | | |
| 3+4: | 3017 | | | | | | | | | | | | | | | | | | |
| 3+5: | 9442 | 4+4: | 4338 | | | | | | | | | | | | | | | | |
| 3+6: | 18755 | 4+5: | 21961 | | | | | | | 3+3+3: | 57 | | | | | | | | |
| 3+7: | 18941 | 4+6: | 32771 | 5+5: | 17512 | | | | | 3+3+4: | 278 | | | | | | | | |
| 3+8: | 8859 | 4+7: | 23810 | 5+6: | 28407 | | | | | 3+3+5: | 173 | 3+4+4: | 327 | | | | | | |
| 3+9: | 1759 | 4+8: | 6847 | 5+7: | 8489 | 6+6: | 5815 | | | 3+3+6: | 86 | 3+4+5: | 306 | | | 4+4+4: | 82 | | |
| 3+10: | 159 | 4+9: | 542 | 5+8: | 825 | 6+7: | 1258 | | | 3+3+7: | 7 | 3+4+6: | 72 | 3+5+5: | 23 | 4+4+5: | 40 | 3+3+3+4: | 1 |
| 3+11: | 3 | 4+10: | 2 | 5+9: | 10 | 6+8: | 19 | 7+7: | 1 | | | | | 3+5+6: | 1 | 4+4+6: | 2 | | |
OEIS
These results extend the table by
Donovan Johnson and Charles R. Greathouse IV on the
OEIS, sequence A207041, which lists Carmichael numbers
that are products of two Carmichael numbers. This extension is twofold: the upper bound 264 is
enlarged to 1024, and products of more than two Carmichael numbers are found.
See OEIS, sequence A387984.
See also OEIS, sequence A214758, which lists Carmichael
numbers that are divisible by another Carmichael number.
Method
In contrast to the bottom-up method described on
OEIS, sequence A207041 (from a list of Carmichael numbers
form all possible pairs below the desired bound, then check the products for Korselt's criterion),
I used a top-down method: first compile tables of Carmichael numbers per number of prime factors
(I simply used the published table
(think before you click, this file is 17.1 GB) of all Carmichael numbers below 1024
published by Andrew Shallue and Jonathan Webster,
up to 1024 there are at most 14 prime factors), then to find the representations with
k Carmichael factors, for k = 2, 3, 4, each Carmichael number n with m
(at least 3k) prime factors is tested as follows: for all possible factors f with
between 3 and m/k prime factors, f is tested by Korselt's criterion, if this
test is positive then the same testing procedure is done for the cofactor n/f with
k decreased by 1, continuing until k has become 1. This method is not only useful when
products of more than two Carmichael numbers are wanted, but also seems pretty efficient for two
factors.
My python program completed the task in 46h 52m 20s running on one core only of the Intel
Core Ultra 9 185H processor on my Asus NUC 14 Pro+. The computation was repeated on the
Saber cluster at TU/e to validate the results.
Examples
Here are two examples with many representations, showing some structure, visualized in a graph.
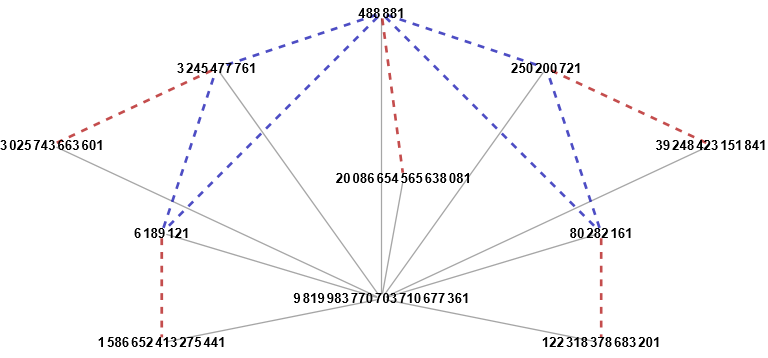
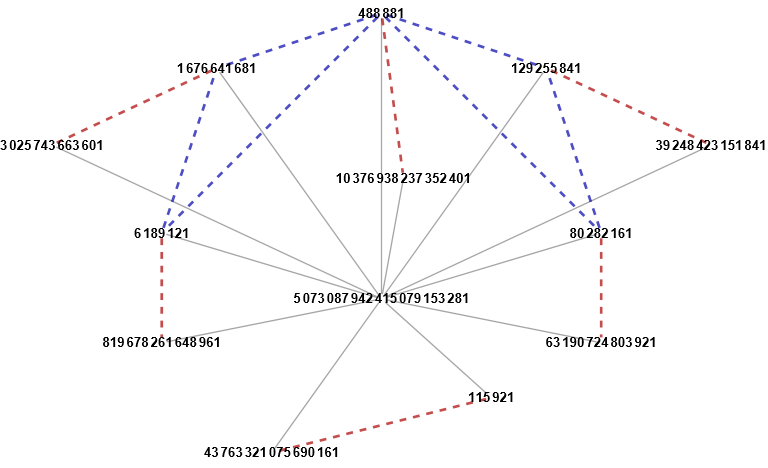
Representations as a product of three Carmichael numbers are visualized as blue triangles,
and representations as a product of two Carmichael numbers are visualized as red lines.
9819983770703710677361 has two representations as a product of three Carmichael numbers,
and five representations as a product of two Carmichael numbers.
5073087942415079153281 has two representations as a product of three Carmichael numbers,
and six representations as a product of two Carmichael numbers.
Note that the structure in both is that for each triangle with numbers a, b,
c (with product a b c = 9819983770703710677361 or
5073087942415079153281 respectively), for each side (a,b) the number c
opposite to that side is one of a representation of two factors (shown as a red line),
where the other factor is equal to (of course) a × b.
Example: in the left hand graph for 9819983770703710677361 there is a blue triangle
on the left with numbers 488881, 6189121, 3245477761. On each of the three vertices
there is a red line, e.g. 3245477761 connects to 3025743663601, which equals
488881 × 6189121.
The two blue triangles have a vertex in common (488881), and therefore there is one
red line serving both triangles, i.e. there is one Carmichael factor of
9819983770703710677361 that has two representations with two Carmichael factors
(here 20086654565638081 = 6189121 × 3245477761 = 80282161 × 250200721).
Also note that the two graphs have not only the basic stucture but also some of the
Carmichael numbers themselves in common.
Questions / Conjectures
Consider the graph with all Carmichael numbers as vertices, and edges whenever one divides another.
Is this graph connected?
Update, 10 Dec. 2025: Daniel Larsen and Thomas Wright tell me that this follows
(by some nontrivial reasoning) from
Thomas's paper and
Daniel's paper. Actually this proves even more:
every two vertices are connected by a path of length at most 4.
Consider the subgraph of all Carmichael numbers that are a product of Carmichael numbers, and
all their Carmichael factors. Is this graph connected?
For each k ≥ 2, consider the graph that has as vertices all Carmichael numbers that
are a product of k Carmichael numbers, and edges between any two such numbers that share a
Carmichael factor. Is this graph connected for each k ≥ 2?
The figure below is the subgraph for k = 3 and Carmichael numbers below 1022.
Of the 254 vertices 252 live in one big component with 3878 edges.

If you wish (and are bold enough), each of these 1 + ∞ unanswered questions can be read
as a conjecture.
Update, 10 Dec. 2025: Daniel Larsen writes me that he believes these conjectures are true.
Author
Benne de Weger, Eindhoven University of Technology, Eindhoven, The Netherlands.
December 9, 2025


