Composite integers with many Euler liars
In [1] we are interested in constructing composite integers
for which the first so many primes are Euler liars. Experimentally we find that
more and more those numbers appear to be Carmichael numbers, and a good way
of treasure hunting is to look at products of Carmichael numbers that themselves
are also Carmichael numbers.
See [2] for all Carmichael numbers up to 1024
that are products of Carmichael numbers. This is exhaustive, while in
[1] the Carmichael products are special ones that are way
larger than 1024.
In [1], Chapter 3, we studied the Euler liar groups for
Carmichael numbers, leading to a classification. See [3]
for the exhaustive classification of the Carmichael numbers up to 1024.
While for Fermat's primality test Carmichael numbers are disastrous, it's nice to see
that for Solovay and Strassen's primality test again Carmichael numbers seem to be
the most obnoxious ones.
The group of Euler liars
In treasure hunting for composite integers for which the first so many primes are
Euler liars it helps to look for composite integers with many Euler liars. Actually
for given composite n the Euler liars form a subgroup 𝓔n
of the multiplicative group ℤn* of integers (mod n).
Let's write I(n) = φ(n) / #𝓔n for
the index of this subgroup in the full group. Clearly we want I(n) to be
small. As there is at least one Euler witness for each composite n we must have
I(n) ≥ 2. In [1], Chapter 3, we proved that
I(n) = 2 for approximately half of the Carmichael numbers, showing why
they are very interesting for our purposes, while the remaining Carmichael numbers have
I(n) = 2m where 2 ≤ m < k, where
k is the number of prime factors of n. We believe the following is true
(see [1], Conjecture 15):
- Open Problem 1: If n is odd and squarefree and I(n) = 2
then n is a Carmichael number.
Sophie Germinus (pseudo)primes
We did a small brute force search for squarefree odd composite integers n <
106 with I(n) = 4, and next to Carmichael numbers we found
only integers of the form n = p(2p-1) where p and 2p-1
both are prime. Primes p such that 2p-1 is also prime have been studied
somewhat, see the OEIS entry [4]. Unlike the very similar Sophie
Germain primes these primes seem to not have been properly named, so (after a suggestion
by Daniel J. Bernstein) we propose the name Sophie Germinus prime for such primes,
and Sophie Germinus pseudoprime for the product p(2p-1) when
p is a Sophie Germinus prime.
In [1], Section 6, we prove that for any Sophie Germinus pseudoprime
n we have I(n) = 4. We believe the following is true
(see [1], Conjecture 15):
- Open Problem 2: If n is odd and squarefree and I(n) = 4
then n is a Carmichael number
or a Sophie Germinus pseudoprime.
The function πSG-(x), counting the Sophie Germinus primes up to x,
conjecturally (see [5]) satisfies
πSG-(x) ~ 2 C2 x / log2x,
where C2 = 0.660161... is the twin prime constant. Asymptotically this is
the same as for the function πSG+(x), counting the Sophie Germain
primes up to x. Just for fun, here is a small table:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|
| πSG-(10i) | 3 | 8 | 35 | 189 | 1166 | 7752 | 56157 | 423521 | 3306171 | 26571998 | 218134071 | 1822880701 |
|---|
| πSG+(10i) | 3 | 10 | 37 | 190 | 1171 | 7746 | 56032 | 423140 | 3308859 | 26569515 | 218116524 | 1822848478 |
|---|
The number of Sophie Germinus pseudoprimes up to x is (conjecturally)
~ πSG-(√(x/2)) ~ 4 √ 2 C2 (√x) / log2x.
This shows that in the long run they are less abundant than Carmichael numbers,
according to the Erdős conjecture that there are
x1-K(log log log x)/(log log x) Carmichael numbers
below x, for some constant K. In the short run however the situation is
reversed, because at the current bound x = 1024 their number is just
≈ x0.3537, which leads to a (questionable) estimate K
≈ 1.8664. The crossover point where Carmichael numbers start outrunning the
Sophie Germinus pseudoprimes then is at about 10625.6, but this
estimate is highly sensitive for small changes in the estimate for K, so is
very questionable.
Unfortunately (?) for the goal of treasure hunting for composite integers for which
the first so many primes are Euler liars, the Sophie Germinus pseudoprimes seem to
behave far worse than Carmichael numbers. That's why in [1], Section 6,
we call Sophie Germinus pseudoprimes the "next best " option and did not
consider them in earlier sections.
Euler liars for RSA numbers
Any n which is the product of two odd primes we call an RSA number, for
obvious reasons (though here we are not concerned with the RSA cryptosystem). We have
the following result for the number of Euler liars for RSA numbers. This generalizes Lemma 14 in
[1].
- Theorem: For n = p q, where p, q are
distinct odd primes, the number of Euler liars in ℤn* equals
½ d2, where d = gcd(p-1, q-1).
In other words, the Euler liar group index in ℤn* equals
I(n) = 2 φ(n) / d2.
A consequence is the result, announced above, that for Sophie Germinus pseudoprimes, which
have d = p - 1, we have I(n) = 4, and this is best possible,
i.e. I(n) > 4 for all other RSA numbers. On the other side of the spectrum
we have Sophie Germain pseudoprimes and twin pseudoprimes as two examples where
d = 2, so there are only 2 Euler liars in those cases.
If we take random primes p, q then typically d is small, so the size
of the Eular liars subgroup of RSA numbers n tends to be small. See the figure below,
which shows for the RSA numbers below 20000 the percentage of Euler liars in the full group.
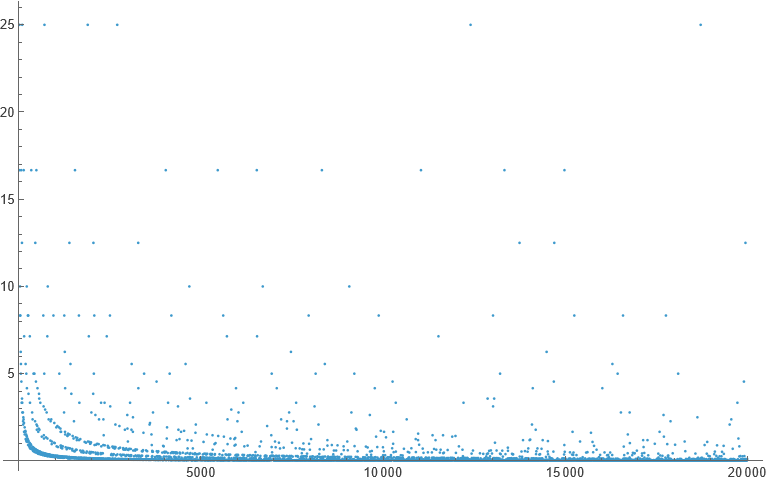
Proof of the Theorem: rsa_eliars.pdf.
Open questions
- What is the (size of the) Euler liars subgroup of ℤn*
for any composite n? The size (or the subgroup index) would make
a nice contribution to OEIS. (For prime n it makes sense to define
I(n) = 1, although the concept of "liar" is a bit weird
in this case.)
- Prove the Open Problems 1 and 2 above. Probably this is within reach.
- Fermat liars also form a subgroup of ℤn* (and a
supergroup of 𝓔n). What can be said about it?
- Strong liars form a subset of Euler liars, in fact, when n ≡
3 (mod 4) the sets are the same. They do not always form a subgroup, when
this happens is known, see [6], Exercise 3.17.
- What about other types of pseudoprimes?
A wealth of information can be found in [7], Chapter 9.
References
[1] Alejandra Alcantarilla Sánchez, Jolijn Cottaar, Tanja Lange,
and Benne de Weger, Ours go to 211: Euler pseudoprimes to 47 prime bases (from
Carmichael numbers), submitted.
[2] Carmichael numbers
that are products of Carmichael numbers.
[3] Classification of
Carmichael numbers.
[4] Primes p such that
2p-1 is also prime, OEIS A005382.
[5] Chris K. Caldwell, An
amazing prime heuristic, arXiv 2103.04483 [math.HO].
[6] Richard Crandall and Carl Pomerance, Prime numbers, a
computational perspective, Second Ed., Springer, 2005.
[7] Eric Bach and Jeffrey Shallit, Algorithmic Number Theory,
MIT Press, 1996.
Authors
Alejandra Alcantarilla Sánchez, Jolijn Cottaar, Tanja Lange, and
Benne de Weger, Eindhoven University of Technology, Eindhoven, The Netherlands.
January 25, 2026
